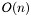where 
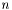is the length of the input string -- one computation per input atom, for the length of the input string.A string is an ordered set of members of an alphabet, of arbitrary size. A string of length zero is called the empty string, and is sometimes referred to as epsilon.
In this context, a language is a set of strings over a given alphabet. It can be finite (finite number of finite-length strings) or infinite (infinite number of possibly infinite-length strings).
A language is decidable if there exists a Turing Machine, which takes any string as input, that will halt and then accept or reject -- accepting if and only if the string is a member of the language. If no such Turing Machine exists, the language is said to be undecidable.
A finite automaton (FA) is an abstract machine consisting of:
A finite automaton is a deterministic finite automaton (DFA) if there are no epsilon-transitions (FA transitions which have epsilon as their input atom) and for each state, for each alphabet member, there is at most one transition. In other words, from any given state, a given input atom can either result in a transition to a single state or cause the input string to be rejected. Because a DFA can only be in one state at any given time, its memory requirements are constant, and they are relatively easy to implement as algorithms. 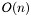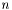Another important feature of DFA-running algorithms is that their runtime complexity is where is the length of the input string -- one computation per input atom, for the length of the input string.
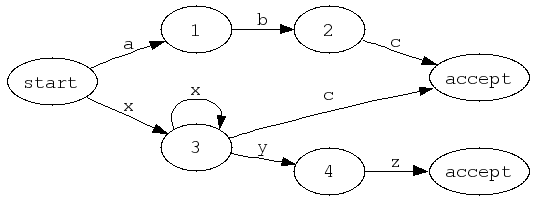
Here is a graphical example of a DFA which accepts the strings "abc", "xc", "xxc", "xxxc", etc, "xyz", "xxyz", "xxxyz", etc. Note that from any state, there is at most one transition for any given input atom.
A finite automaton is a nondeterministic finite automaton (NFA) if it is not a DFA -- if there are any epsilon transitions, or multiple transitions from a given state for a given input atom. This means that an NFA can potentially be in many states at once. For example, if there were two transitions from the current state which accept the same input atom, the next "current state" would actually be the set of target states of each exercised transition -- the current state set. Note that a set cannot have duplicated members. If there were two different states which both transitioned into the same state, the resulting current state set would be the single target state identified by both the exercised transitions. Because an NFA's current state set can potentially have as many members as it has states, its memory requirements are not constant. Implementing an algorithm which runs an NFA is more difficult than for a DFA, because more computation (e.g. epsilon-closure) must be done by the algorithm. The runtime complexity of an NFA-running algorithm is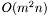 
where 
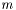is the number of states and 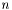is the length of the input string -- up to 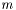possible members in the current state set, each transitioning to at most 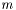states, once per input atom, for the length of the string.
Here is a graphical example of an NFA which accepts the strings "ac", "abc", "ax", "axx", "axxx", etc, and the empty string. Note that from some states, there are multiple transitions using the same input atom. There are also epsilon transitions indicated by the transition label (e).
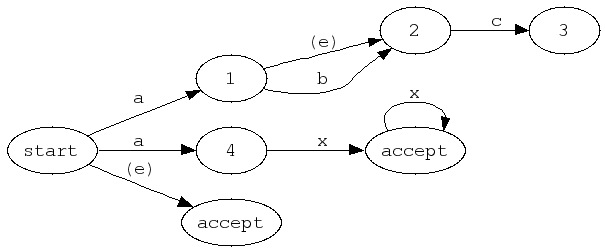
There exists an algorithm called the subset construction algorithm to convert any NFA into a DFA. It essentially involves calculating every possible current state set reachable from the starting state. Each unique current state set reachable in this manner is mapped into a single state in the DFA. This is a useful result because one can convert any NFA into an easy-to-implement-and-run and fast-running DFA.
Because of the result provided by the subset construction algorithm, the classifications NFA and DFA are equivalent. Forthwith, FA refers to the generic classification of finite automata, which includes the equivalent classifications NFA and DFA.
A language is a regular language if and only if there exists an FA which decides it. In other words, if and only if there is a FA which accepts all strings in the language and rejects all strings not in the language, then the language is regular.
A regular expression (regex) is a syntactical form for compactly specifying a regular language. See Generic Regular Expressions (The Boring Kind) for more information. Because each regex specifies a regular language, for each regex there exists an FA which decides if a string is accepted by the regex. It is straightforward to construct an NFA from a regex, and using the subset construction algorithm, generate an equivalent DFA.
TODO: write about DPDAs, NPDAs
TODO: write about context-free languages and their NPDAs, and the deterministic CFL subset and their DPDAs.
TODO: write about ASTs
The nesting of language classifications indicate that the contained classification is a subset of the containing one. Regular languages are the most limited and are a subset of everything, and are consequently the most simple and easiest to implement algorithmically. Context-free languages are the immediate superset of regular languages and require what's known as a pushdown automaton (PDA) to decide them. Therefore, anything decidable by an FA is decidable by a PDA. reflex uses regular languages via regular expressions to implement an FA to decide input. trison uses context-free languages via Backus-Naur form grammars to implement a PDA to decide input. A PDA is just an FA with an auxiliary memory stack. If it weren't for certain extensions in reflex (e.g. ^ and $ and other conditionals), any scanner FA written using reflex would be equivalent to some parser PDA in trison.
TODO: make sure above paragraph is consistent with the TODOs in the previous section
TODO: subset algo
TODO: modified NFAs
TODO: modified subset algo
TODO: modified DFAs
1.5.1